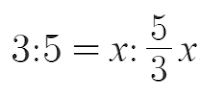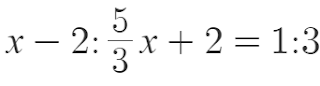My preliminary response to instructing this was, how? I had my very own elaborate algebraic procedures, however I had been chastised up to now by the scholars for reaching for algebra at any time when the going received robust, it wasn’t one thing that was coming to naturally to college students. After which, if you work this out by hammering it with algebra, you have been sort of disillusioned – like there have to be a quicker approach.
My preliminary response to breaking this down then was to record equal ratios, and that is nonetheless one thing I like to recommend to college students after they don’t know what to do. In the event you do that the reply drops out fairly quick:
What if that they had 3:5 – you’d get 1 and seven – this doesn’t work.
What if that they had 6:10 – you’d get 4 and 12 – this does work.
Don crushes the concept that this might be a cinch with the subsequent one:
This takes lots longer. High-quality – we’d like one other technique. That is the place we come across the “what a part of the ratio stays the identical” method. The variety of marbles Kim has stays the identical so we will evaluate the ratios like this:
Initially: 5:6 = 40:48
Later we come to an issue once more – and if we’d regarded again at Anthony and Cleopatra we’d have famous {that a} technique of issues being mounted wouldn’t actually have labored for us.
Till I used to be launched to what was truly mounted – and on this case our mounted half was our variety of socks – the whole of the ratio.
So initially we’ve got: 9:5:14
And subsequently we’ve got 3:2:5
Earlier than: 9:5:14 = 45:25:70
After: 3:2:5 = 42:28:70
So every a part of the unique ratio is 3 pairs of socks, so we’ve got 135 white pairs of socks and 75 pairs of purple socks.
And that is the place I assumed the story ended, with a stunning easy common technique for these issues – resolve what you need to be mounted and repair every thing in keeping with it. Then I used to be in a coaching session and somebody caught up these questions and requested us to have a go at them, earlier than sharing the algebraic strategies that his college students did.
And I scoffed and went “oh ho ho, how enlightened I’m realizing a greater approach..!”
There was a dialogue across the Sine Rule on Twitter just lately the place the opinion was aired that as maths lecturers we generally tend to “algebratise” every thing too rapidly. I’m undecided I noticed it at the beginning of my profession, however I feel I are likely to agree now. Isn’t there one thing to be mentioned that maths lecturers do “algebratise” although? And the way will we develop that as a ability?
What about that ‘higher approach’ I used to be so smug about? It leads us to the reply, however is it simply an endpoint? The place does this result in? In truth I thought of, what if actually these questions are a stunning car for additionally introducing some algebraic work? Even after the ‘common’ technique has been launched there’s working available on taking part in round with algebra in these questions and taking part in round with how we introduce unknowns.
So going again to the unique query:
Initially:
Afterwards:
So:
What about if the whole was x?
A possible stepping stone from ratio to algebra depends upon the fashions you utilize for ratio. I have a tendency to construct from a “containers” technique of ratio to display 3:5 as
The place the open field is a vessel that has to comprise the identical as all the opposite containers.
If we use that open field as x then we’re fixing a query the place x is one a part of the unique ratio, and we will apply that to the Asterix and Cleopatra drawback.
Initially:
Then:
So:
In conclusion, not every thing must be ‘algebratised’ and infrequently different numerical methods of fixing issues may give you options to issues in elegant methods. Nevertheless, the reply needn’t be the top and exploring totally different algebraic methods of exploring these issues may also help your college students fluency and competency with algebra.