Angle bisection, incircles and reasoning with ratios

This ‘Dose of Don’ is totally different
in flavour to my earlier posts. As an alternative of following what has been stimulated
for me in Don’s work I’m following a thread of his personal inquiry.  For a workshop on angles he introduced some
duties that relied on defining an angle by its tangent ratio. I talked about
this in my first ‘Dose of Don’ weblog as he had a concept that for those who approached angle by limiting it to those who
might be expressed on a sq. grid, then many angle and trigonometric information,
and different geometrical insights, might be deduced in particular instances and that
attainable generalisation to all angles might be explored.  The angles that may be expressed on a sq.
grid and people whose trig ratios could be constructed on the lattice factors, e.g.
in triangles for which a number of the aspect lengths could be expressed as rational multiples
of one another. To simplify this he restricted exploration at first to these angles
whose tangent ratio was ‘on the grid’, so angles are an inverse of ratios, not
but expressed in levels or radians.

OK thus far?

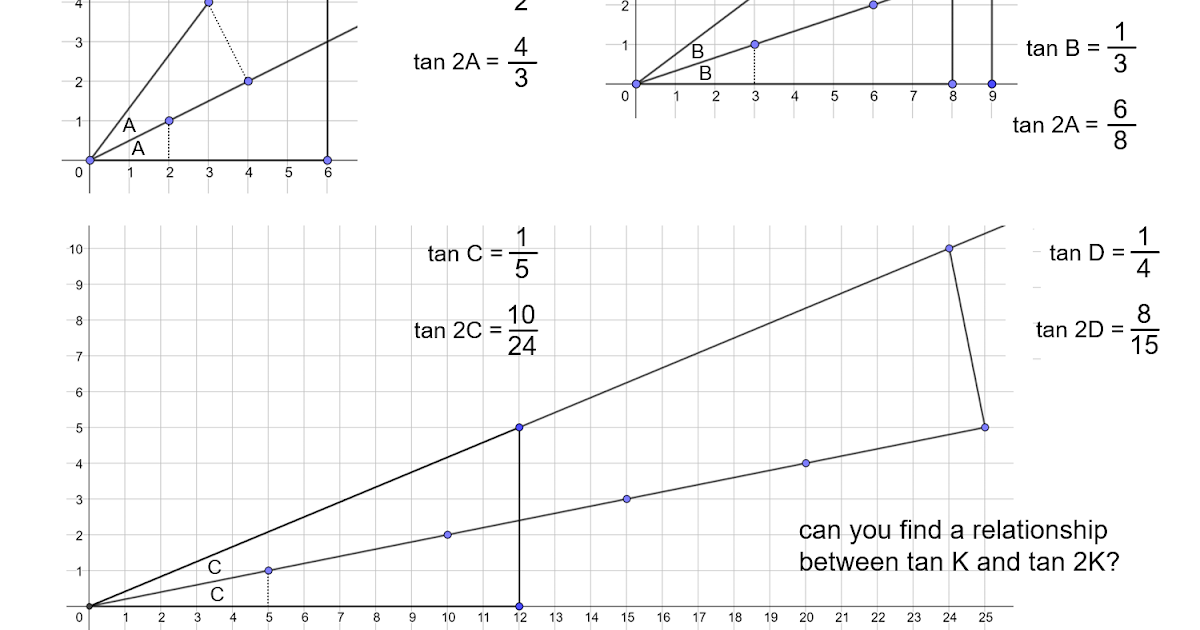
Then he started to discover angle
bisectors.  I had forgotten this
route however discovered it once more whereas tidying my desk and discovering my scribblings. Most
of what I discovered is at : https://donsteward.blogspot.com/search/label/anglepercent20bisector

He begins by suggesting you utilize a
compass/straight edge strategy to bisecting an angle and observe whether or not and the place
your bisector passes by lattice factors.  There may be then the next abstract slide
about what you might need discovered (a typo for tan B/tan 2B is straightforward to identify).

Now the rationale I had put this to at least one aspect for over a yr is as a result of my data of double angle formulae is strong even 60 years after I first met them and this gave the impression to be getting in the best way of imagining how learners would possibly reply the query a couple of relationship between Ok and 2K. May I actually reconstruct a relationship I knew with out utilizing it as a ‘purpose’? In different phrases, may I deal with the Ok query as a goal-free downside? I may select options of the diagram and make sure them by utilizing current data. I don’t recall, nonetheless, ever utilizing the tangent double angle components to search out the tangent of a half-angle – the knowledge I have to bisect angles on the grid. After some manipulations I came upon how to do that and realised that that is how Don should have developed the actual examples he supplied and why (you’ll have observed this) they appeared to wish Pythagorean triples to ‘work’. However I’ve not answered for myself the query of how anybody who was not conversant in double-angle formulae would possibly strategy the bisection query.

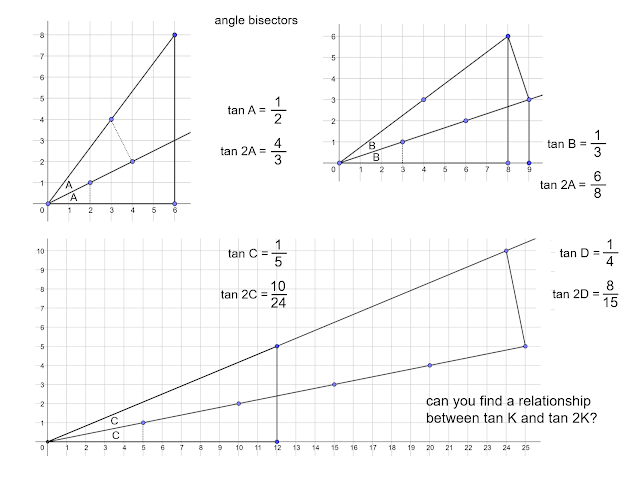
One other strategy to strategy the
bisection query is to make use of data of incircles to do some reverse
reasoning: if angle bisection provides me the incentre, then the incentre will
give me clues about angle bisectors. Triangles on grids, notably
right-angled triangles with their legs on the grid, supply a number of reasoning
routes and – hey presto! – the tangent ratio for the half-angle plops out
earlier than your very eyes!

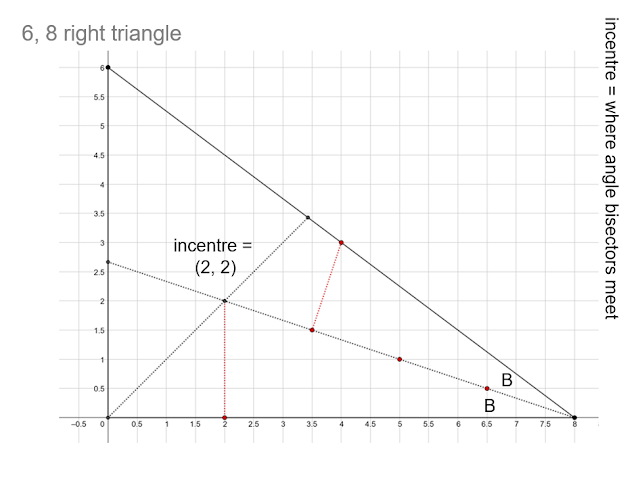
This line of reasoning will depend on
some strains of thought that could be extra acquainted than inverse tan and Don’s
slide quantity 30 can take you there.  It
is a free-standing exploration that will depend on realizing about areas of triangles
and Pythagoras.

A diagrammatic strategy I
notably like follows:

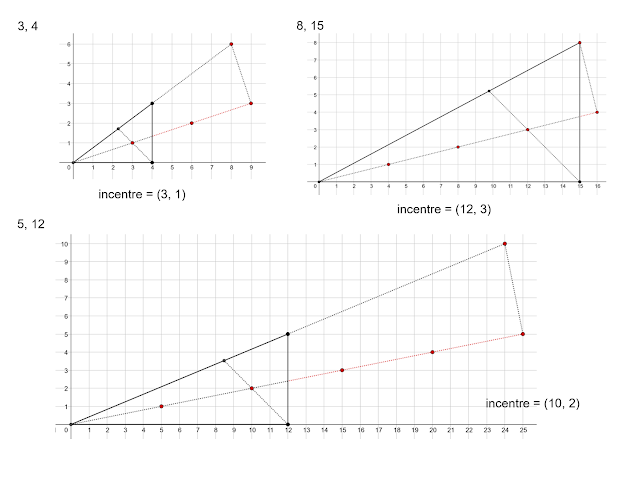
I discovered it’s attainable to purpose the connection between the half angle and the complete angle with out serious about incentres however as a substitute by reasoning with ratios. To point out that the 2 half angles are equal (and subsequently should be halves of the complete angle) I solely have to point out that their tangents are equal, i.e. that their defining ratios are equal. The unit lengths by which the ratios are constructed don’t matter. I like this. For me, it’s about looking for comparable triangles utilizing lattice factors.

Throughout our time with Don, John Mason and I raised a difficulty that has been hanging round for years: reasoning with ratios could be very highly effective however we hardly ever see diagrams from which ratio ‘jumps out’ clearly as an vital underlying relationship. We can not ‘see’ ratio; we have now to purpose it out. I suppose the identical could be stated for multiplicative relations extra usually; we can not ‘see’ them in the identical method as we are able to ‘see’ addition or distinction. We predict Don labored on this in his grid duties however by no means had a dialog with him about it. Nevertheless, I’ve discovered 4 diagrams that recommend he had discovered one thing. I can not discover them on his web site however perhaps haven’t been trying in the suitable place. I’ve reconstructed them right here, as a result of my copy is roofed with my scribbled workings-out which might be a distraction (e.g. ‘can’t see ratios’, ‘attempt 3:2 alongside hyp’ and so on.)

Lastly, you probably have bought this far, a pedagogic query: how
do the variation and invariance in these 4 diagrams assist or hinder
understanding and generalising the underlying relationships?